GTO 3/4/5 betting pt.2
Posted by vanity02
Posted by
 vanity02
posted in
Gen. Poker
vanity02
posted in
Gen. Poker
GTO 3/4/5 betting pt.2
We'll now find the optimal strategy pair for Alice and Bob when Alice open-raises from early position (EP =UTG or MP), and it's folded to Bob in position.
It's of course possible to vary EP opening ranges a lot, according to opponent tendencies and general game conditions. But the core strategy for a typical TAG is to open somewhere around 15% of his hands (plus/minus a couple of percentage points in both directions) from both EP positions, and slightly tighter from UTG than from MP.
We'll construct all strategies/ranges with great detail for this scenario, so that there won't be any doubt about how to apply the theory. Then we'll move on to the scenario with Alice in CO, and do this quickly, with brief comments along the way.
3.1 Alice's optimal raising strategy in EP (UTG and MP)
We assume Alice is opening with a ~15% EP range. Note that any 15'ish% EP-range will do, since our work is based on the numbers of hands in the range, and not the specific hands it contains. Obvious value hands like high pairs and AK have to be included, since these hands have a job to do in the ranges for 4-betting and calling 5-bets. But the exact mixture of medium and weak hands in Alice's range is irrelevant.
We give Alice the following range:
Alice's EP range
22+
ATs+ AJo+
KTs+ KQo
QTs+
J9s+
T9s
98s
87s
76s
186 combos
14%
We now place Bob somewhere with position on Alice. Alice open-raises and it's folded to Bob, who 3-bets. Both players want to play perfectly against the other, and both assume the other is also trying to play perfectly.
Alice starts by defining her value range. This is per definition the hands she plans to 4-bet for value and then call a 5-bet with. She counts the total number of combos in her opening range (186), and she knows that she on average has to defend 30% of her total range against a 3-bet. She also knows that the optimal value/bluff ratio of her 4-betting range is 60/40. So she 4-bets 0.60 x 0.30 =18% of her opening range for value, and 0.40 x 0.30 =12% as a bluff.
Alice then 4-bets 18% of the 186 combos for value, e.g. 0.18 x 186 =33 value combos. This corresponds almost exactly to the value range {QQ+, AK} =34 combos (a couple of combos too many or too few doesn't matter much). This is a standard value range from EP, also for players who haven't studied optimal raise/3-bet/4-bet/5-bet strategies.
Now the 4-bet bluff range. These are the hands Alice 4-bets and then folds to a 5-bet. There are two ways to define the bluff 4-bet range: We can choose some specific bluff combos and always 4-bet them, or we can 4-bet all the non-value hands a certain % of the time.
Let's illustrate both methods:
Defining a 4-bet bluff range using the combo method
If we choose specific bluff combos, we need 12% of 186 combos, e.g. 0.12 x 186 =22 bluff combos. For example, we might choose AQ (16) + JJ (6) which gives us exactly 22 combos. Or we can choose something different, since it doesn't matter what we use for bluffs when Bob either folds or 5-bets all-in. When Bob doesn't fold to our bluffs, he 5-bets, and we have to fold, so our 4-bet bluff hands never get to see a flop. And when they never get to see a flop, their postflop value is irrelevant.
But note that a hand like AQ works as a blocker against Bob's premium hands (AA, AK, QQ). So when Alice uses AQ as a bluff, it will be less likely that Bob has a hand he can 5-bet for value. Keep this in mind if you are choosing specific hands to always use for 4-bet bluffing.
Defining a 4-bet bluff range using the percentage method
My preferred method, and also the easiest method to remember. We only need to remember one number, namely the static percentage Alice 4-bet bluffs her non-value hands. Let's find this percentage once and for all:
Alice 4-bets 18% of her opening range for value, and she's left with 82% non-value hands she can use for 4-bet bluffing. We now choose to use all these hands a fixed percentage of the time, so that the effective total value/bluff ration is 60/40. We now want:
value/bluff =60/40
18/82x =60/40
18/82x =1.5
18/82 =1.5x
0.22 =1.5x
x =0.22/1.5 =0.15 =15%
So we 4-bet bluff all non-value hands 15% of the time and fold them the remaining 85% of the time. Note that this percentage is universal for Alice. No matter what her opening range is, she can always use this percentage to obtain a 60/40 value bluff ratio for her 4-bets.
Let's double-check to see that this works the way it should:
When Alice has raised some opening range and gotten 3-bet, we have deduced that her optimal value 4-bet range is 18% of her total range. If she 4-bets the remaining 82% of her range as a bluff 15% of the time, her overall bluff percentage will be 0.15 x 0.82 =0.12 =12%. So her total 4-bet range is he optimal 18 + 12 =30%, with a 18/12 =60/40 value/bluff ration. So the percentages add up perfectly.
Alice's optimal raise/4-bet/call 5-bet strategy in EP
We now have everything we need to specify Alice's total strategy after a 15% open-raise. We can write Alice's total EP range as a sum of value hands (raise, 4-bet for value, call a 5-bet) and bluff hands (raise, 4-bet bluff, fold to a 5-bet):
{Alice's total EP range}
={22+,ATs+,KTs+,QTs+,J9s+,T9s,98s,87s,76s,AJo+,KQo}
={value hands} + {4-bet bluff hands}
={QQ+, AK}
+ (15% 4-bet and 85% fold) x {the rest of the range}
Alice raises {22+, ATs+, KTs+, QTs+, J9s+, T9s, 98s, 87s, 76s, AJo+, KQo} =186 combos from EP. If she gets 3-bet, she 4-bets {QQ+, AK} for value and calls a 5-bet with them. Those times she doesn't have a value hand, (e.g. she has JJ, AJo, 76s, etc.), she 4-bets 15% of the time as a bluff, and otherwise she folds.
The percentage of value hands is then 34/186 =18%, while the effective percentage of bluff hands is 0.15 x (186 - 34)/186 =12%. The value/bluff ratio for her 4-bet range is 18/12 =60/40, which is optimal.
To randomize her 4-bet bluffs and get the correct 15% 4-bet frequency for her non-value hands, Alice uses a random number generator from random.org. She has this on her screen in a small browser window:
Let's illustrate randomized 4-bet bluffing in practice with an example:
Example 3.1.1: Randomized 4-bet bluffing in EP
$100NL
6-handed
Alice ($100) raises pot to $3.50 with 6 6 from UTG, it's folded to Bob ($100) on the button, who 3-bets pot to $12. The blinds fold, and Alice has to make a decision. 4-bet or fold?
Alice does not have one of her value hands {QQ+, AK}, so she knows that this is a 4-bet-bluff-or-fold scenario. She also knows how often she should 4-bet bluff with these hands (15%). Alice clicks the random number generator, planning to 4-bet to 27bb ($27) if it returns a number between 0 and 15, and otherwise she folds.:
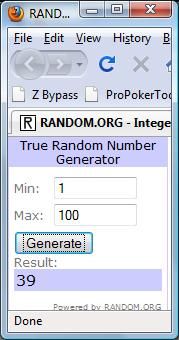
The randomize returns 39, so Alice folds this time.
We have now specified Alice's optimal EP strategy for for raising/4-betting/calling a 5-bet when she gets 3-bet by a player in position. Our next step is to turn to Bob. What is Bob's optimal strategy for 3-betting/5-betting in position after a ~15% EP raise from Alice?
3.2 Bob's optimal 3-bet-strategy versus Alice's optimal raising strategy in EP
We're assuming Bob knows Alice's opening range (he only needs to know the % of hands, not the specific hands), either from observation, or by using a HUD. Alice's raise percentage dictates her value 4-bet range, which dictates Bob's strategies for 3-betting and 5-betting.
Bob starts by finding the hands that he 3-bets and 5-bets all-in, purely for value. His value range also includes some 5-bet bluffs, and the next step is to find these. Then we pick a range of 3-bet bluffs that Bob plans to fold to a 4-bet. We'll also talk about Bob's flatting range. These are medium strong hands that are playable, but they are not strong enough to 4-bet for value,and they are too strong to use as bluffs, so Bob flat-calls with them.
Bob's flatting range can be viewed as a completely separate part of Bob's overall strategy, and we don't have to be concerned with it when constructing optimal ranges for 3-betting/4-betting/5-betting. But we will discuss the flatting range briefly, since it helps us understand the big picture. When Alice has raised, Bob can respond in 3-ways: He can 3-bet (for value or as a bluff), he can flat, or he can fold. Different hands have different jobs to do within these ranges. And depending on Alice's opening range, hands can move between Bob's 3-betting/flatting/folding ranges.
For example, we'll see that AK isn't strong enough to be a value hand for Bob against Alice's EP range, so AK goes into the flatting range in this scenario. But when Alice opens a much wider ~25% range in CO, AK is promoted to a value hand that is 3-bet and 5-bet for value. More about that later in the article.
So let's begin defining Bob's optimal 3-bet/5-bet strategy in position against Alice's optimal raise/4-bet/call 5-bet strategy with a ~15% EP range:
Bob's pure value range
Bob knows that Alice EP range is ~15% (14% to be exact), and therefore he can draw the same conclusion Alice just did, namely that her optimal value 4-betting range is {QQ+, AK}. To profitably 3-bet and 5-bet all-in for value against this range, Bob needs a hand with at least 50% equity.
AA is obviously such a hand, and we can easily compute some equities to see that KK is the only other possible hand. So Bob ends up with the super tight pure value range {KK+}.
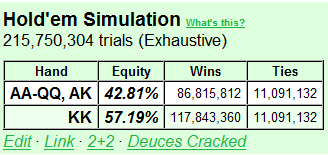
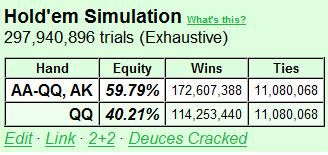

So Bob will 3-bet {KK+} and 5-bet them all-in if Alice 4-bets. He will also 3-bet/5-bet some 5-bet bluff hands (type Axs), and he will have a wide range of 3-bet bluffs that he folds to a 4-bet. We'll now find Bob's 5-bet bluffing hands, then his 3-bet bluffing range, and then we are done.
But first, let's talk about something that I know you're thinking about right now:
Wait a minute, are you saying that we shouldn't 3-bet the mighty strong QQ and AK for value against an EP open-raise?
Correct. Against Alice's tight and optimally played ~15% EP opening range, QQ and AK aren't strong enough to use as value hands, even if they have strong equity against Alice's total opening range. The reason is that they can not profitably get the whole stack in Against the range Alice is willing to get all-in with, namely {QQ+, AK}. Therefore we don't want to 3-bet them for value. Keep in mind that the process of getting all-in starts with a 3-bet, and we know the moment Alice open-raises with a ~15% EP range that her all-in range is a favorite over our QQ and AK hands.
Therefore, since we know this before we have put our first chip into the pot, we don't want to choose a path with QQ/AK that is the first step towards getting all-in with them preflop. This is also true for other hands that are good enough to play for value, but not strong enough to get all-in preflop against Alice's value range {QQ+, AK}. Examples of such hands are QQ-22, AK-AJ, KQ, QJs-T9s, etc. (and you can probably list some more if you think about it).
So should we 3-bet these medium strong hands as bluffs then?. No, because they are too strong to turn into bluffs and waste their postflop value. The alternative, which is a good one, is to flat-call with them and play a raised pot with position against a range we have god equity against (namely Alice's total opening range). Of course, we could always pretend they are trash and use them as 3-bet bluffs, but why should we do that when it's profitable to flat and play for postflop value? It's true that we want to 3-bet bluff a lot, but we have plenty of bad hands to choose from for that purpose, and we don't want to waste the postflop value we gain from flatting with our medium strong hands.
Here is a soccer analogy in these World Cup times:
Moving QQ/AK from the flatting range up to the value range against a ~15% opening range is a bit like moving a defender forward and using him as a striker. Sure, he might score a goal or two, but he isn't quite good enough for the job. But he is too good to sit on the bench, so he should play. Therefore, since there is another job for which he is well qualified (defending), we let him play there. The right man for the right job.
Bob will therefore flat QQ, AK and various other medium strong hands/implied odds hands after a ~15% open-raise from Alice. The optimal flatting range depends on how Bob thinks Alice plays postflop, what he thinks the players in the blinds will do, how they play postflop, their stack sizes, etc. So we leave the construction of an optimal flatting range to Bob.
Note that 3-betting QQ and AK for value against a ~15% EP raiser is equivalent to assuming the raiser isn't playing optimally. If you feel these two hands can always be 3-bet and 5-bet all-in for value against this EP range, you can assume it's because the players you meet don't defend well against 3-bets out of position.
Thinking about these things is useful, because when we know what's game theoretically correct, we know that we can exploit someone if it seems correct to do something else. So feel free to deviate from optimal play in Bob's place, if you have position on a weak player. For example, you might be up against a player who 4-bet bluffs spazzy and way too much, or he raises a lot and calls 3-bets out of position with medium strong hands, and then he plays fit-or-fold on the flop. Against such players, QQ and AK might be used as value 3-bet/5-bet hands, since our opponents play far from optimally against our 3-bets.
But don't 3-bet QQ/AK for value against a ~15% opening range in the hands of a player like Alice. She plays optimally against our 3-bets, so 3-betting QQ/AK won't do anything for us. Against Alice we use QQ/AK as flatting hands, thus setting ourselves up for playing a raised pot in position against a range we have good equity against (Alice's total opening range, and not just her value hands). This will give Alice (and the blinds, should they get involved) opportunities to make postflop mistakes that we can exploit.
But later in the article we'll let Alice open with a ~25% range from CO, and we'll see that QQ/AK now moves up to Bob's value range. Alice's value range is wider and weaker with a 25% opening range, and Bob's optimal 3-bet strategy changes accordingly.
OK, enough about flatting. Let's move on and find Bob's 5-bet bluffs, and then his 3-bet bluffing range:
We include 5-bet bluffs in Bob's value range
Remember the definition of "value range" as the hands we 3-bet, planning to 5-bet all-in after a 4-bet. Some of these hands will be 5-bet bluffs, but for simplicity we'll refer to all the 5-betting hands as Bob's value range.
From the previous theory section, we remember that Bob wants to have enough Axs 5-bet bluffs in his value range to make Alice's weakest value hands break even. This accomplishes two things for Bob:
• He forces Alice to fold more of her 4-bet bluffs
• He makes it impossible for Alice to "cheat" by not paying off Bob's value 5-bets with {KK+}. If she tries to be "smart" and fold QQ/AK, Bob will just collect his profit with his 5-bet bluffs instead.
So Bob's 5-bet bluffs with some Axs hands attack Alice's 4-bet bluffs, and they also make it impossible for her to profitably tighten up her value range, even if she knows Bob's value range is the squeaky tight {KK+}. Keep in mind that Alice knows Bob's strategy, since this follows from her own strategy, which follows from her opening range, which both players know.
So she knows Bob only 3-bets/5-bets {KK+} for pure value, and if Bob's doesn't 5-bet bluff a bit, Alice can improve her 5-bet-calling strategy by folding the big underdog's QQ/AK from her value range {QQ+, AK}. And when one of the players can improve his/her EV by a strategy change, the original strategy pair can't be optimal (per definition). So Bob has to 5-bet bluff.
The next step for Bob is to add enough Axs to make Alice's weakest value hands break even when they call a 5-bet. Alice then calls off her last 73bb to win the blinds + Alice's 4-bet + Bob's stack =1.5 + 27 + 100 =128.5 bb. The pot odds are 128.5 : 73 =1.76 : 1, so Alice needs minimum 1/(1 + 1.76) =36% equity against Bob's 5-betting range to call profitably.
We add A5s to Bob's value range, and check Alice's equity with QQ/AK:
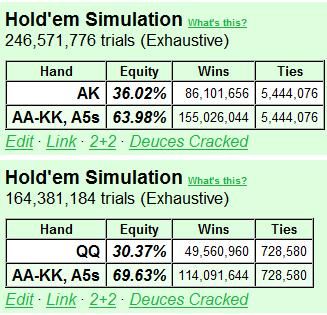
AK is above the threshold, but QQ is way below 36%. We add A4s and try again:

QQ is now slightly better than break even, and Bob can use A5s/A4s as his optimal 5-bet bluffing hands. However, if we want Alice's equity to be exactly break even, we have to remove a 5-bet bluff or two. Let's remove A 4 and see what we get:

Bingo, and Bob's optimal 5-bet bluffing hands are {A5s, A 4 , A 4 , A 4 }. But here I'll say that we don't have to be this strict. A combo or two too much or too little doesn't change things much, and we can use A5s/A4s in practice. Also, as we'll discuss further in the summary at the end of the article, it's debatable whether we need to 5-bet bluff at all in most games, unless we are playing against people like Durrrr.
People generally don't 4-bet bluff enough, and they are also reluctant to tighten up their 4-bet value ranges when they get exploited by very tight 5-betting (e.g. 5-bets that are 100% for value). For example. a typical low limit TAG with a ~15% EP range might have decided to never 4-bet bluff, and always 4-bet QQ and AK for value and call a 5-bet with them. And he is unlikely to change that plan, even if Bob's exploitative response is to drop all 5-bet bluffs from his value range, and only 5-bet-shove {KK+}, purely for value.
These things happen because a) people are blinded by seemingly strong hands, even after they get trapped in situations where their hands suddenly aren't strong anymore, and b) because people are reluctant to change their initial plan, even after if becomes clear it's a bad plan.
Against an opponent who makes the dual mistake of not 4-betting bluffing enough, and also paying off our value 5-bets too much, Bob can gain a lot from not having to think about 5-bet bluffing. Bob simply 3-bets {KK+} for value, plus a wide range of 3-bet bluffs, and after a 4-bet he 5-bets {KK+} for value and folds everything else.
This way Bob exploits Villains lack of 4-bet bluffing, since his 3-bet bluffs forces Villain to fold most of his non-value hands (since Villain is unwilling to 4-bet bluff with these hands). And Bob also doesn't need to attack Villain's 4-bet bluffs with 5-bet bluffs of his own, since Villain isn't 4-bet bluffing. Finally, Bob exploits Villain's static 5-bet-calling range by only 5-betting for value (and getting called as a big favorite), and not having to include 5-bet bluffs for deception. Easy game.
At any rate, Bob's final value 3-bet range (including his 5-bet bluffs) against Alice's optimally played ~15% EP range is {KK+, A5s, A4s}. Bob's last job is to construct the 3-bet bluff range. These are the hands we 3-bet, and always fold to a 4-bet.
Bob's 3-bet bluff range
We remember the strength principle for poker hands:
- Bet/raise your strongest hands for value
- Check/call with your medium hands
- Fold/bluff with your weakest hands
We have already defined Bob's value range (including 5-bet bluffs) as {KK+, A5s, A4s}, and we have mentioned that he also flats some range of good-but-not-great medium strong hands. Against Alice's ~15% EP range this means flatting with hands like QQ, JJ, TT, AK, AQ, AJ, KQ, etc.
So when we pick hands for Bob's 3-bluffing range, we drop down to the "cellar" and pick hands that aren't god enough to 3-bet for value preflop, and not good enough to flat for postflop value. Against Alice, who either 4-bets or folds, it doesn't matter which hands we choose to 3-bet bluff with, since these hands will never see a flop. Alice either 4-bets or folds, and when she 4-bets, we 5-bet our value range all-in, and fold our 3-bet bluff range.
But in practice the choice of 3-bet bluff range matters a bit, since the raiser will sometimes call our 3-bet with his medium strong hands out of position and force us to play postflop. Therefore, since we can choose freely from our worst hands, we might as well choose the best of our worst hands.
In other words, we'd rather 3-bet a hand like K8s as a bluff than a hand like 72o. K8s has some postflop value those times the raiser calls and forces us to see a flop, while 72o doesn't. So 3-bet bluffing with hands like K8s dominates (e.g. is sometimes better than, and never worse than) 3-bet bluffing with hands like 72o.
So let's list some 3-bet bluff candidates à la K8s that are too weak to flat, but have some postflop value when we get called. We make a list of ace high, king high and queen high candidate hands:
Candidate list for 3-bet bluffing:
- Ace high: A9s-A6s ATo-A8o (52 combos)
- King high: K9s-K6s, KJo-K9o (52 combos)
- Queen high: Q9s-Q6s, QJo-Q9o (52 combos)
If you don't approve of this list, feel free to make your own. The specific hands are irrelevant, what matters is that we use hands with the right properties, namely hands that aren't quite strong enough to flat. NB! A5s-A2s are reserved for 5-bet bluffing, so we can't include them in this list.
This gives us a list of 156 "pretty" combos for 3-bet bluffing, and the next question is which hands to choose and when. We remember that the optimal value/bluff ratio for Bob's 3-betting range is 40/60, so he can use 60/40 =1.5 bluff combos for each of the combos in his value range (including his 5-bet bluffs). His total value range is {KK+, A5s, A4s} =20 combos, so Bob can pick 1.5 x 20 =30 3-bet bluff combos.
As mentioned previously, there are two techniques Bob can use:
- Pick 30 specific combos and always 3-bet them
- 3-bet all hands from the candidate list a certain percentage of the time
I prefer the percentage method. To use it, we only need to memorize the candidate range once and for all, plus one number (the % we 3-bet bluff the candidate hands). Let's compute the number to use against Alice's EP range:
To effectively have 30 bluff combos from the candidate list in our 3-betting range, we need to use each of them 30/152 =20% of the time. Note that this percentage isn't universal, like Alice's fixed 4-bet bluff percentage (15%) is for all her opening ranges. To see this, note that Bob's value range varies with Alice's opening range, but the candidate list of 3-bet bluff hands is static (we have simply chosen some hands to use).
So Bob will have to calculate a new bluff% to use for his candidate list against each of Alice's opening ranges. However, this isn't a big job, we simply do the math once and for all against each of Alice's ranges and memorize the numbers we need (and we'll look at Alice's CO range in a minute).
So, finally:
Bob's optimal 3-bet strategy against Alice's optimal raising strategy in EP
{Bob's total 3-bet range}
={value hands and 5-bet-bluff hands} + {3-bet bluff hands}
={KK+, A5s, A4s}
+ 20% x {A9s-A6s,ATo-A8o,K9s-K6s,KJo-K9o,Q9s-Q6s,QJo-Q9o}
Bob always 3-bets {KK+, A5s, A4s} and 5-bets all-in after a 4-bet. If he has one of the 152 combos from his candidate list for 3-bet bluffing, he uses a randomizer and 3-bet bluffs 20% of the time, and he folds to a 4-bet. We had to do a bit of work to construct all these ranges, but it was worth it, and we have learned a lot in the process.
Let's see what Bob's optimal total 3-bet% is in this case:
- Value part: 20 combos (1.5% of all hands)
- Bluff part: Effectively 20% of 152 =30 combos (2.3% of all hands)
This results in a total 3-bet% of 1.5 + 2.3 =3.8% against Alice's ~15% EP raises. His value/bluff ratio is the desired optimal 20/30 =40/60. Later, when we construct an optimal strategy against Alice's 25% CO range, we'll see that Bob's 3-bet% skyrockets as a consequence of Alice raising a much wider opening range.
Note that the combination of a candidate list of 3-bet bluff hands and a fixed (but adjustable) bluff% to use with these hands, gives us a lot of flexibility to adjust our 3-bet bluffing as we please. Against an unknown opponent, we can start with the optimal 20% frequency, and 3-bet {KK+, A5s, A4s} always, and the candidate list 20% of the time. But if we note that the raiser doesn't defend optimally, we might want to adjust this bluff percentage.
For example, of the raiser never 4-bet bluffs and only 4-bets a tight value range like {QQ+, AK}, we can go bananas with our 3-bet bluffs. We might decide to double the bluff frequency from 20% to 40% for our list of 152 bluff candidate combos. Now we have 20 value combos, and effectively 0.40 x 152 =61 bluff combos. This means 20/(20 + 61) =25% of our 3-bets are for value, and 75% are bluffs. Our first adjustment to exploit this particular opponent is therefore to lower the optimal value/bluff ratio from the optimal 40/ to the more exploitative 25/75.
Then we can also drop 5-bet-bluffing against this tight player, as discussed previously. The simplest adjustment is to keep 3-betting our 5-bet bluffing hands A5s/A4s, but we move them from the value range down to the 3-bet bluff range, and fold them to a 4-bet. The only hands we 5-bet against this player and his {QQ+, AK} 4-bet range is {KK+}, purely for value.
Here is an example of randomized 3-bet-bluffing, using the randomizer from random.org:
Example 3.2.1: Randomized 3-bet bluffing against a ~15% EP raise
$100NL
6-handed
Alice ($100) raises to $3.5 from UTG, and it's folded to Bob ($100) who has Q 9 on the button. This hand is on the candidate list of 3-bet bluff hands, and we remember that the optimal bluff frequency to use against a ~15% opening range is 20%. Bob clicks the randomizer, planning to 3-bet if it returns a number between 0 and 20, and otherwise fold:
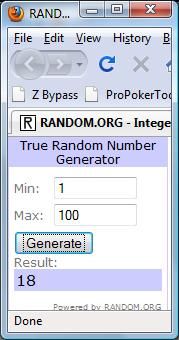
The randomizer returns 18, so Bob 3-bets to $12. Alice quickly 4-bets to $27, and Bob folds.
Everything according to plan, and with total control, so there is no reason to feel frustrated after this clash. Our Q 9 did it's job (attacking the weakest part of Alice's opening range) perfectly, regardless of the outcome, and it's irrelevant that Alice had a 4-betting hand this time.
Remember that we know Alice's strategy just as well as she knows our strategy, and we know that she will 3-bet us 30% of the time and fold 70%. When the 4-bet comes, we quietly fold our 3-bet bluffs and 5-bet-shove our value/5-bet bluff range of {KK+, A5s, A4s}. And we do these things calmly, without emotion.
By en.donkr.com "bugs"
Loading 0 Comments...
Be the first to add a comment
You must upgrade your account to leave a comment.
This thread has been locked. No further comments can be added.